Here’s a puzzler: Why are the Common Core math standards accused of fostering “fuzzy math” when their drafters and admirers insist that they emphasize basic math, reward precision, and demand fluency? Why are CC-aligned curricula causing confusion and frustration among parents, teachers, and students? Is this another instance of “maximum feasible misunderstanding,” as textbook publishers and educators misinterpret the standards in ways that undermine their intent (but perhaps match the interpreters’ predilections)? Or are the Common Core standards themselves to blame?
My take is that the standards are in line with effective programs, such as Singapore Math, but textbook publishers and other curriculum providers are creating confusion with overly complex explanations, ill-written problems, and lessons that confuse pedagogy with content.
Many of the “fuzzy math” complaints seem to focus on materials that ask students to engage in multiple approaches when tackling arithmetic problems. But to understand whether the confusion stems from the standards or the curriculum, let’s start by recalling what the CCSS actually require.
1. The Common Core explicitly demand student mastery of the standard algorithms for addition, subtraction, multiplication, and division for both whole numbers and decimals.
Any honest reading of the standards must recognize that in grades 4, 5, and 6, the Common Core demand that students master standard algorithms. In grade 4, students should “fluently add and subtract multidigit whole numbers using the standard algorithm.” By grade 5, they are expected to multiply whole numbers using the standard algorithm. And by grade 6, they are expected to divide whole numbers and to add, subtract, multiply, and divide decimals, again using standard algorithms.
The standards themselves are unambiguous that students will master the best and most efficient ways to do arithmetic, and any curriculum that does not give top billing to standard algorithms in the pertinent grades is not aligned with the Common Core.
2. The Common Core also allow more than the standard algorithms.
Because math users and teachers want more than procedural fluency from students (because they want young people actually to understand the math problems they answer so that they are ready for more advanced math), the Common Core leave plenty of room for teachers to go beyond the standard algorithm to ensure that students understand how numbers work. The standards ask that students understand what it means to add to and subtract from; the difference between parts and a whole; and to be able to demonstrate these understandings in more than one way.
For example, beginning as early as first grade, students are expected to
… use a variety of models, including discrete objects and length-based models (e.g., cubes connected to form lengths), to model add-to, take-from, put-together, take-apart, and compare situations to develop meaning for the operations of addition and subtraction, and to develop strategies to solve arithmetic problems with these operations.
More specifically, a first-grade standard asks students to
Add within 100, including adding a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used.
Here, students are not limited to lining up numbers, carrying the one, or borrowing but are able to use manipulatives or drawings to arrive at answers or illustrate their understanding of what it means to add or take away one. This video gives a clear sense of how a student might use a “10 frame” or number cubes to count and to add, and it shows how useful such a model can be in helping students learn numbers.
Indeed, as the video demonstrates, such “modeling” has long been part of traditional math programs such as Singapore Math. And the appropriate, efficient use of modeling and drawing helps students understand numbers and can help them solve increasingly complex problems.
Here’s another example drawn from Singapore Math, in which a drawing is used to help pupils make sense of an elementary subtraction problem:
? – 7 = 5
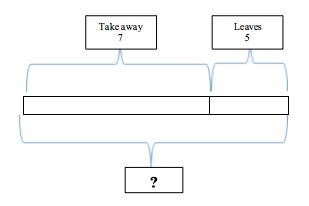
In this problem, students are encouraged to draw the whole—which is unknown—and to show what they know. That is, some number minus 7 leaves 5. In this case, the drawing is used as a tool to better understand what the problem is asking. While a student should ultimately be able to answer problems of this sort without visual aids, this kind of “modeling” can help lay the foundation that students need to solve increasingly complicated problems through the grades.
Such “models” can be even more useful for students when it comes to making sense of fractions and answering fraction problems. Take, for example, this middle school problem, also drawn from Singapore Math:
Ronnie had 90 fish. He sold 1/2 of them and gave 1/3 of them to his friend.
- What fraction of the fish was left?
- How many fish did he give to John?
Whole

Whole, divided into six equal parts
![]()
Answer:
- First, change to fractions with like denominators. (2/6, 3/6)
- Next, using the model, show the portions sold and the portions given to John.
![]()
Using the model, it’s easy to see that Ronnie has 1/6 left.
Unfortunately—but perhaps predictably—as more publishers work to align their math programs to the CCSS, there is ample room for screw-ups. And comedian (and New York City parent) Louis C.K. gave several examples of blunders when he complained to his 3 million followers that the Common Core curriculum at his daughter’s school—with its bewildering math problems and related tests—was making her cry.
He also tweeted a few examples, including this one:
6 students are reading books for book clubs. They are reading one of the following stories:
Story A: Matilda
Story B: Magic Tree House Lions at Lunchtime
Story C: Superfudge1/2 of the students are reading Story A.
1/3 of the students are reading Story B.
1/6 of the students are reading Story C.In the model below, each box represents one student in the group. Complete the model based upon the information above. Write one letter A, B, or C in each box to represent the story each kid read.
![]()
Answer:
![]()
Louis C.K. is right: this problem (along with some others he tweeted) is confusing. Yet the confusion doesn’t arise from the math; it’s the fault of the English. The problem includes students (who have no names), book titles, letter labels for the books that are different from the titles, all buried in a problem that is meant to be about comparing fractions with unlike denominators. It would be easy for a student to lose his or her way and get frustrated amidst that information even if s/he gets the math.
Worse, in this example, the model or drawing has become the “goal.” In the Singapore examples, the drawings and models are means to clear-cut ends. They aim to clarify and focus on answering the problem. In other words, the model is used in service of understanding and answering a clearly defined problem.
Ultimately, math should focus on precision. If models confuse more than the math itself, they have lost their utility.
Note, too, that the Singapore problems—typical of what I’ve seen in Singapore Math—are text-lite. The emphasis is on numbers, manipulating numbers, and problem solving. In too many other examples, including those shared by Louis C.K., the math drowns in a sea of confusing text. In short: if you need that much text to explain why or how to use a mathematical model, you’re doing it wrong.
Three takeaways:
First, schools who’ve had long success with tried and true approaches, including Singapore Math, might consider sticking with them before pouring lots of money into shiny new—but possibly ill-written—curricula.
Second, publishers should emulate the clarity and precision of Singapore Math rather than reinventing the wheel and coming up with one that doesn’t roll straight. If they fail in that quest, nobody should buy what they’re selling.
Third, Common Core supporters need to understand that even as opponents eagerly pounce on any mistake that anybody makes in the name of the Common Core, that doesn’t mean that we deny or ignore such failures. Failure is an important part of innovation and a necessary step in the quest for excellence. Indeed, that we should be more exacting critics than the opponents, taking pains not to explain away implementation challenges, mistakes and missteps. Let’s resolve to be vigilant, candid, and demanding in our assessment and communication of such challenges.



